EEM-272 Makine Öğrenmesine Giriş

2024-2025 Bahar Dönemi

Ders 2

Slaytı için tıklayınız.
Video ders (ingilizce).

Univariate (Tek değişkenli) Lineer (Doğrusal) Regresyon

import matplotlib.pyplot as plt
import numpy as np

sizes=np.array([2600, 3000, 3200, 3600, 4000]).reshape((-1,1))
prices =np.array([550000, 565000, 610000, 680000, 725000]).reshape((-1,1))
sizes.shape, prices.shape

    ((5, 1), (5, 1))

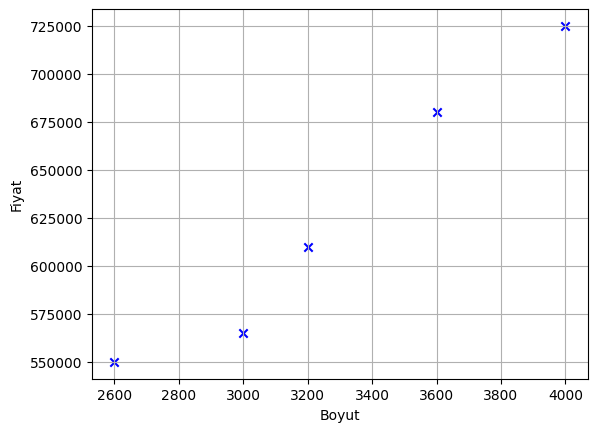
plt.scatter(sizes, prices, marker='x', color='b')

plt.xlabel('Boyut')
plt.ylabel('Fiyat')

plt.grid(True)
plt.show()

png

Lineer regresyon

from sklearn import linear_model

#model
reg = linear_model.LinearRegression()

# modeli verilerle eğitme
reg.fit(sizes,prices)

reg.predict([[3300]])

    array([[628715.75342466]])

# theta_0 değeri
reg.intercept_

    array([180616.43835616])

# theta_1 değeri
reg.coef_

    array([[135.78767123]])

theta_0 = reg.intercept_[0]
theta_1 = reg.coef_[0,0]

# dolayısıyla tahmin fomulu
f=theta_0+theta_1*sizes

f=theta_0+theta_1*3300
f

    628715.7534246575

# tum veri setini tahmin etmek için
prices_pred = reg.predict(sizes)

from sklearn.metrics import mean_squared_error, mean_absolute_percentage_error
print("Ortalama kare hatası: ", mean_squared_error(prices, prices_pred))
print("Ortalama mutlak yüzde  hatası: ", mean_absolute_percentage_error(prices, prices_pred))

    Ortalama kare hatası:  186815068.4931509
    Ortalama mutlak yüzde  hatası:  0.019201242020345188

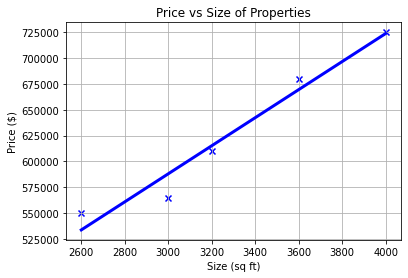
plt.scatter(sizes, prices, marker='x', color='b')

plt.xlabel('Size (sq ft)')
plt.ylabel('Price ($)')
plt.title('Price vs Size of Properties')
plt.plot(sizes, prices_pred, color='blue', linewidth=3)
plt.grid(True)
plt.show()

png